 |
Apple and Orange |
I was curious if I could produce an autostereogram containing
colored objects—something as close as possible to a true-color
autostereogram. In Apple and Orange I tried to color the
apple red, the orange orange, and the shelf they’re sitting on
brown. |
 |
Wooden Chair |
I was wondering if it’s possible to produce an image that’s
simultaneously an autostereogram and an anaglyphic
stereogram (to view through red-cyan glasses). Wooden
Chair is my first attempt to produce such a unified stereogram.
The anaglyph image looks good, but I wish that the autostereogram
were crisper. |
 |
Beach Ball |
This is an experiment in including (faux) transparency in stereographic
images. In Beach Ball, note how the ball has red spots in
front and purple spots in back, and you can see the purple spots
through the transparent red spots. I like how this image turned
out. |
 |
Pottery Sale |
This image represents an attempt to combine a wallpaper
stereogram and a single-image stereogram. In Pottery Sale,
the pottery is a wallpaper stereogram while the back wall and the
front of the table are both single-image stereograms. |
 |
Memories |
I wanted to see if it’s possible to use more than one tiled
pattern in a single image. (Answer: yes. 😀) Notice how
in Memories, the pattern fades from an alphabet in the
upper-left corner to raspberries in the upper-right corner to dice
in the lower-right corner to roses in the lower-left corner. |
 |
Who’s on Top? |
Let your eyes diverge when looking at this wallpaper stereogram.
You should see the array of cubes floating above the array of
spheres, which in turn are floating above the patterned background.
Rotate the image (or your head) 90°. You should now see the
array of spheres floating above the array of cubes, which in turn
are floating above the patterned background. I’d love to perform a
similar trick with a single-image stereogram but don’t know how. |
 |
Bowl of Gems |
Like Pottery Sale above, Bowl of Gems combines
a wallpaper stereogram and a single-image stereogram.
However, Bowl of Gems places the wallpapered objects (gems)
on top of the object represented by the single-image
stereogram (a bowl). Not only that, but different gems appear at
different depths based on the depth of the underlying bowl. (That
took a lot of trial and error, incidentally.) |
 |
Empty Table |
In Empty Table I used a single tiling pattern
throughout the stereogram but varied the brightness. The result is
an image that includes both illuminated and shadowed regions. |
 |
Scattered Shards |
I struggled for a long time to find a way to produce a
stereogram that can be tiled both horizontally and vertically. All
of my attempts ended up being flickery and hard to focus on.
Eventually I gave up trying to tile arbitrary objects and limited
myself to abstract shapes, which are a lot easier to deal with. You
can see the result of my efforts in Scattered Shards.
Maximize your browser window to get the full effect. |
 |
Lovesick |
I was aiming for minimalism here—just a few dots on a
solid background. Unfortunately, making the 3‑D image sufficiently
clear required a lot more dots than I had intended. The good news
is that I found that I could create a nice transparency effect
à la Beach Ball (above) by superimposing two
stereograms: one showing the top half of the object and one showing
the bottom half of the object. |
 |
Winter Scenes |
This may seem like an ordinary stereogram. However,
it’s really a subtle experiment with color. Once you’ve viewed the
stereogram, try converting the image
to grayscale then normalizing the
gray levels. The result probably isn’t what you’d have
expected. |
 |
Exclamation Mark |
I’ve made some progress towards the goal mentioned in
conjunction with Who’s on Top? (above): developing a
single-image stereogram that contains a different image when rotated
90°. Exclamation Mark portrays a boxy exclamation mark
lying within a crease. Rotate the image (or your head) 90°, and
the exclamation mark vanishes while the crease remains. The rotated
image isn’t super-crisp, but I’m pleased that the basic effect seems
to work. |
 |
Stonehenge |
Like Bowl of Gems (above), this image superimposes a
wallpaper stereogram over a single-image stereogram. The difference
is that in Stonehenge the wallpapered image (a line of
people—who were supposed to be druids, but that’s beyond my
artistic ability) not only changes depth but also rotates as it
repeats from left to right. |
 |
Every Which Way |
Aha! I finally figured out how to produce a stereogram that can
be horizontally and vertically tiled yet can portray arbitrary
shapes. While the approach used in Scattered Shards
(above) handles only abstract patterns, my new approach is far more
flexible. Every Which Way successfully represents a bunch
of 3‑D arrows pointing in different directions. Maximize your
browser window to get the full effect. |
 |
Put on a Happy Face |
When not viewed wall-eyed, single-image stereograms normally
appear as a tiled pattern with some distortion (or as random dots
that obscure the tiling and distortion). I wanted to see if I could
produce a single-image stereogram comprising
exclusively undistorted shapes. Put on a Happy
Face is the result. Note how it looks like an unassuming grid
of emoticons, but diverge your eyes, et
voilà!, a 3‑D image emerges. For contrast,
an alternate version of Put on a
Happy Face shows what the stereogram would look like with
the usual distorted-tiling approach: uglier 2‑D but crisper
3‑D. |
 |
The Color of Music |
Observe how the colors in this image vanish when viewed as a
stereogram. Pretty neat, huh? I aligned complementary colors in
such a way that they cancel each other out when overlapped, and that
seems to have worked exactly as intended. |
 |
String Theory |
Is it possible to draw a single-image stereogram without taking
your pen off the paper? String Theory demonstrates that it
is. An SVG version of String
Theory is also available as further evidence that
single-image stereograms do not necessarily have to be bitmaps;
vector graphics can work as well. |
 |
Spider and Web |
New autostereogram artists quickly learn that thin lines are
imperceptible when viewed in 3‑D. I wanted to see if I could
include thin lines in an autostereogram and make them viewable by
altering the 2‑D pattern to enhance their visibility.
Spider and Web is my first attempt to do this. The thin
lines that constitute the spider’s web aren’t perfect, but I believe
they do demonstrate the feasibility of the technique. |
 |
Tintinnabulation |
Tintinnabulation takes the notion of
an ASCII
stereogram one step further. It demonstrates that an
autostereogram can be constructed from undistorted,
proportionally spaced text merely by adjusting
inter-character spacing and dropping characters when necessary. (In
case you don’t recognize the text, it’s the first 1½ stanzas
of Edgar Allen Poe’s, The
Bells.) Note that the
PDF version of the Tintinnabulation
stereogram is fully searchable. |
 |
Rotated Squares |
This one was a surprise to me. I was experimenting with
rotation to see how well the eye can tolerate changes in angle in an
object-array stereogram. I didn’t expect to see the wavy pattern
that emerges when Rotated Squares—comprised entirely
of evenly spaced and equal-sized but differently rotated
squares—is viewed in 3‑D.
An SVG version of Rotated
Squares is also available. |
 |
Row of Trees |
Row of Trees is what’s called an object-array
stereogram , which means that there’s no hidden 3‑D image.
Instead, when the picture is viewed wall-eyed, the (visible) objects
in the image take on depth. What makes Row of Trees
different from other object array stereograms is that it was created
entirely from photographs taken at different angles, with no
3‑D computer modeling. The depth you perceive is therefore
the natural depth of the scene. |
 |
Child’s Play |
This is an attempt to combine two types of stereograms:
hidden-image stereograms and object-array stereograms. The small
toys repeated throughout the picture have depth when viewed in
3‑D but are also positioned at precise heights so as to define
a large 3‑D image. The small objects exhibit less depth than
I would have liked, but I believe that overall this is a good proof
of concept. |
 |
Caged Creature |
The idea here was to superimpose an object-array stereogram atop
a conventional, hidden-image stereogram. What makes this
interesting is that the object in the object-array stereogram
is in fact a hole through which the conventional stereogram can be
seen. The rest of the object-array stereogram is solid black. |
 |
Magic Hat |
The only interesting thing here is that the 2‑D pattern fades
from showing a normal Abracadabra on the right side of the
image to a reversed Abracadabra on the left
side of the image. |
 |
One Cent |
This hidden-image stereogram is a photograph, only minimally
retouched (straightened, cropped, resized, and white balanced). The
things I learned from this exercise are that (1) it’s really
tedious laying out dozens of pennies on a sheet of paper, and
(2) with a 19mm diameter, pennies form rather large pixels.
Consequently, I was able to make the underlying height map only
10×8 pixels—0.01% of the resolution of most of the other
stereograms on this page. In case you can’t decipher the 3‑D
image, it’s supposed to say 1¢ on a sloped
background. |
 |
Butterfly |
This stereogram is both horizontally and vertically symmetric.
Flip it across either Cartesian axis, and it will look the
same. |
 |
Snowflakes |
When viewed in 3‑D, one snowflake appears higher than the
other in this object-array stereogram that is also a valid
QR code. The
snowflakes are a little hard to focus on—perhaps try each in
turn—but the stereogram does work well as a proof of concept.
I used Russ Cox’s QArt
Coder to produce the QR code. |
 |
King Me |
Like Put on a Happy Face (above), King Me is
an attempt to construct a stereogram entirely out of undistorted
shapes. Unlike Put on a Happy Face, however, King
Me allows the shapes to overlap, which produces a crisper
image. The 3‑D image, which is supposed to be a crown, isn’t
as detailed as I’d like, but that’s a subject for a future
stereogram. |
 |
We All Scream |
The idea here was to combine the coloring of Apple and
Orange, the transparency of Lovesick, and the
undistorted shapes of King Me. Unfortunately, the
3‑D image, which is supposed to be an ice-cream cone, is a bit
abstract and, quite frankly, doesn’t look nearly as nice as I would
have liked. |
 |
Goldfish Bowl |
Here’s a fun stereogram that even the stereogram-impaired can
enjoy as it’s both a stereogram and an optical illusion.
The
3‑D image is a basic object-array stereogram but with the
objects skewed a bit in the z dimension using the trick I
discovered when developing
Rotated Squares (above). In the the 2‑D image, a
school of goldfish appears to move slowly in a wave pattern but is
in fact quite stationary. (The optical illusion was inspired
by Akiyoshi
Kitaoka’s Murasaki-imo wave . I enjoy many of
Prof. Kitaoka’s works.) |
 |
Straight Lines |
Following the theme of Goldfish Bowl (above), I wanted
to see if I could combine stereograms with other types of optical
illusions. In Straight Lines, the optical illusion is that
the checkerboard pattern is perfectly straight and regular, even
though it looks crooked. The 3‑D image is, alas, just a
boring diamond shape. I wasn’t able to achieve the resolution
needed to do better without sacrificing the optical illusion. |
 |
Room and Mushroom |
I had wanted to do something like this for a long time and
finally figured out how. Room and Mushroom shows different
3‑D images at different zoom levels. When viewed at 100% zoom
(1920✕1080 pixels), the image depicts a living room. When
scaled down to 25% (the equivalent of 480✕270 pixels), the
image depicts a large mushroom. The living-room images
unfortunately contains some distracting coloration; use the top
guides to help focus (and use the bottom guides to help focus on the
mushroom). A DjVu version
of Room and Mushroom lets you separately display the
foreground (living room) and background (mushroom) images. |
 |
Fun and Games |
Is it possible to create a stereogram whose 2‑D image is a
maze? The answer is sort of. In Fun and Games, the
3‑D image is supposed to
be Pac-Man, but
it’s unfortunately rather hard to identify and even rather hard to
focus on. Use the ghosts at the top to help align your eyes. The
2‑D image isn’t too terrible, though. For the solution to the
maze, load the
SVG version of Fun and Games
into Inkscape and mark
the Solution layer as visible. |
 |
Ode to Quadrilaterals |
This stereogram shows four quadrilaterals popping out of a
concave background. What’s interesting here is that the 2‑D
image is itself composed entirely of quadrilaterals, all with crisp
borders. An
SVG version of Ode to Quadrilaterals
is also available. |
 |
Cubism Bear |
I wanted to see if it’s possible to make a stereogram in which
the background pattern portrays a recognizable object, challenging
the requirement that a background pattern be a repeating
tile. Cubism Bear overlaps partial images of a teddy bear,
as might be done in a cubist painting, to accomplish this feat. |
 |
Flower Photo |
Like Room and Mushroom (above), Flower Photo
presents different 3‑D images at different zoom levels. The
difference lies in the interpretation of the smaller image. When
viewed at 100% zoom (1024✕768 pixels), Flower Photo
is a hidden-image stereogram of a camera. When scaled down to 25%
(the equivalent of 256✕192 pixels), Flower Photo
changes from a hidden-image stereogram to a side-by-side stereogram
(i.e., image pair) of a flower. |
 |
Two Monets |
Continuing the theme of Room and Mushroom
and Flower Photo (above), Two Monets represents a
combination of two images. In this case, the 3‑D image is
Monet’s Grainstack,
Sun in the Mist, and the 2‑D image—best viewed
at a distance—is
Monet’s In
the Garden. Although it’s a little hard to focus on the
3‑D image, Two Monets does show that it’s possible to
superimpose a non-repeating 2‑D image on a stereogram without
completely destroying the 3‑D effect. |
 |
Household Items |
The defining characteristic of a wallpaper stereogram is
repeated images. But can one produce a wallpaper stereogram in
which no image is repeated? Household Items is
based on images morphing into each other—a pencil into an
umbrella, a clock into a hat, etc.—sufficiently gradually so
as not to disrupt the 3‑D effect. I’m pleased this works as
well as it does. |
 |
Big Snake Mouth |
A single-image stereogram’s 2‑D tiles are typically
discontinuous across repetitions. The effect is particularly
noticeable for tiled photographs. For Big Snake Mouth I
tried to make the tiling seamless. Although successful, I had to
sacrifice sudden changes in depth in the 3‑D image, which is a
severe limitation. |
 |
Sombrero |
This stereogram is an experiment in overlapping multiple
3‑D images at different depths. Notice how, especially near
the center of the image, the red mesh is raised above the white
mesh, which is raised above the green mesh. I like this effect
although I don’t think I did such a great job modeling a
sombrero. |
 |
Traffic Jam |
Here, I was trying to render a traffic light with red, yellow,
and green spheres floating above a gray base. After more than 40
completely failed attempts, I gave up trying to crisply separate the
colors and accepted some color bleed between the lights and the
base, which is what you see here. Anyway, an
SVG version of Traffic Jam is also
available. |
 |
Graph Graph |
Graph Graph began with an attempt to draw stereograms out of
triangles but degenerated into a sophomoric play on words: a graph
(vertices connected by edges) 2‑D pattern that produces a
graph (bar chart) stereogram. An
SVG version of Graph Graph is also
available. |
 |
River Canyon |
This is mainly an experiment in mixing extreme and subtle
changes in depth, represented respectively by the tall cliffs and
the gentle waves on the river. The color blend between the cliffs
and the river worked out nicely, too. |
 |
Great Pyramid |
Here’s my to-scale rendering of
the
Great Pyramid of Giza, constructed entirely from colored
triangles—7488 of them, to be exact. (I initially tried
modeling all three pyramids in the Giza pyramid complex, also to
scale, but the 3‑D didn’t work out as well as I had hoped.)
An
SVG version of Great
Pyramid is also available. |
 |
Desk |
Many computer-graphics formats are based on 24-bit color: 8 bits
for each of the red, green, and blue color channels for a total
palette size of 28 ×
28 × 28 = 16,777,216 colors.
What makes Desk unique is that it uses each of those
16,777,216 colors exactly once. (Thanks
to Michael Fogelman’s
AllRGB script for automating the color assignment.) At
4096×4096 pixels (and 45 MB), Desk is a much
larger stereogram than most of the others on this page. It’s best to
view the image at full size and scroll around to see all the
3‑D items. A ray-traced, full-color
version of the 3‑D model may help you identify what you’re
looking for. Desk was a fun stereogram to produce because
it allowed for much greater detail to be modeled than is possible
with smaller images. |
 |
Sinking Ship |
Unlike probably every other single-image stereogram ever
produced, Sinking Ship is drawn with concentric circles,
centered roughly in the middle of the picture. I’m pleased with how
well this image came out, and I’m in fact amazed that using
concentric circles instead of a horizontally repeated pattern works
at all. |
 |
Pretzel Maze |
This stereogram revisits the question posed above by Fun and
Games: Is it possible to create a stereogram whose 2‑D
image is a maze? By improving upon the technique introduced
with Big Snake Mouth, I was finally able to create an
honest-to-goodness maze that is also an easy-to-focus-on
autostereogram. (Try to navigate from the upper-left corner to the
lower-right corner.) Admittedly, the maze isn’t the most
interesting maze ever created, and abrupt changes in depth are
lacking from the 3‑D image, but I nevertheless
consider Pretzel Maze a resounding success. An
SVG version of Pretzel Maze is also
available. |
 |
Locks and Keys |
Like Winter Scenes above, Locks and Keys is an
attempt to conceal a 2‑D image within what looks like an
ordinary random-dot stereogram. To see the hidden image this time,
map the stereogram to polar coordinates.
(In GIMP,
use Filters→Distorts→Polar Coordinates….)
Stand back a few paces, and behold! |
 |
Secret Message |
Can you read the secret message? It’s a bit flickery, but look
for text written vertically down the middle of the image. |
 |
Secret Message 2 |
Here’s an easier-to-read secret message. An
SVG version of Secret
Message 2 is also available. |
 |
Faces and Vases |
Do you see pictures of faces or vases? (Look particularly at
the top and bottom rows.) Here, I wanted to see if I could
incorporate
a Rubin
vase—with my own shaggy profile— into an
autostereogram. An
SVG version of Faces and
Vases is also available. |
 |
Rainy Night |
This started as an experiment of different depth layers (a bit
like Sombrero, above), but I was unable to make it work as
intended. In the end, I removed the fancy stuff, leaving only the
pleasant, if ordinary, stereogram you see here.
An SVG version of Rainy Night
is also available. |
 |
Black Hole |
Black Hole is more like what I was originally shooting
for with Rainy Day, above. Note how the 1000+ stars
depicted in this image appear in 3‑D at such a wide variety of
depths. The nearby stars at the edges of the image are somewhat
cluttered, making them a bit hard to focus on, but the stars in the
center are quite crisp. An SVG version
of Black Hole is also available. |
 |
Herringbone Necktie |
One problem with single-image autostereograms is that the
2‑D image’s tile pattern normally winds up being discontinuous
in spots. Contrast Herringbone Necktie
with what it would have looked like
with typical stereogram-generating software. Notice how the
thick, diagonal lines in Herringbone Necktie are
preserved—with some distortion but no
disjointedness—across the entire 2‑D image. In
contrast, the alternative version presents a crisper 3‑D but
at the cost of a more broken 2‑D. |
 |
How to Design an Autostereogram |
This idea was too cute to pass up: a flowchart showing how to
design an autostereogram. You start with the basic concept, then
use 3‑D modeling software to produce a grayscale depth map.
If this looks good, you create a 2‑D tiling pattern. Once
you’re happy with that, the next step is to produce the
autostereogram from the depth map and the tiling pattern. If the
result is hard to focus on, a different tiling pattern may help.
Sometimes, the autostereogram works fine but is simply
uninteresting, in which case you start all over.
An SVG version of How to Design an
Autostereogram is also available. |
 |
Turtles All the Way Down |
Can one create a stereogram in which the 2‑D tiling
pattern is another stereogram? Why not? Turtles All the Way
Down depicts a 3‑D turtle. Zoom in to 800% to see that
each tile is a stereogram of the same 3‑D turtle, itself
tiled by little, colored 2‑D turtles. I’d recommend
downloading the
large JPEG version of Turtles All
the Way Down (18 MB) or
the large DjVu version
(10 MB). At 8192×6144 pixels, these are substantially
crisper than the 1024×768 version. In either case, the top
and bottom of the image are the least distorted so zoom in there
first. |
 |
Pool Table |
In the past, I’ve observed that if the near-plane and far-plane
repetition distances in pixels exceed a 2:1 ratio, the 3‑D
image is hard to perceive. Pool Table uses a 6:1 ratio
globally but ensures that very near and very far objects are not
placed close to each other. The result is a stereogram that
exhibits quite a range of depth. The colors at the top of the image
repeat every 200 pixels while the pixels at the bottom of the image
repeat only every 30 pixels. Contrast this
to a version of Pool Table
with more typical far-plane/near-plane
separation—repetition distances ranging from 102 to 128
pixels, as is used in many of the images on this page. (I sometimes
go to 85–128 but rarely beyond that range.) |
 |
Apple Tree |
This is a stereogram of a stylized apple tree. What makes it
interesting is that it is composed entirely of differently colored
and differently scaled ellipses. An SVG
version of Apple Tree is also available. |
 |
Kilroy Was Here |
This isn’t my best 3‑D, but if you stare enough at the
bottom half of the image you should be able to perceive
Kilroy
and his elongated proboscis peering over a wall. More interesting,
however, is the 2‑D image of
an impossible
trident. Note how the ten rectangular prongs at the bottom
blend into twelve cylindrical prongs (plus a few off-screen) at the
top. |
 |
Jailbirds |
Here’s another stereogram that can also be enjoyed by the
stereogram-impaired. Either print out the image and cut it on the
dashed lines into three pieces or view
the interactive, online version
of Jailbirds. Count the number of rectangles. You
should get 28. Now swap the top two pieces and count again. This
time, there are only 27! Where did the 28th rectangle go? Also,
note that the stereogram works in both the original and rearranged
configurations. Neat, huh? |
 |
Eye |
Can a stereogram establish its 3‑D image out of
negative
space? My best answer so far is yes, but with very low
resolution. Eye comprises a set of thick, colored
lines that are evenly spaced horizontally, but carefully placed gaps
define a cartoon eye when viewed wall-eyed.
An SVG version of Eye is also
available. |
 |
Ring of Sauron |
There’s a lot going on in this text stereogram. First,
it comprises exclusively valid English words. (I had to rely on a
fair number of those
dubious two-letter
Scrabble words, though.) Second, the lines of
the One
Ring’s inscription appear alternately on the left and right.
Third, a 3‑D annulus pops out of the main part of the image.
Fourth, the caption, the one ring pops out of the bottom part
of the image. A plain-text version
of Ring of Sauron is also available. |
 |
Rock Cairns |
Although he creates a lot of great stereograms,
3Dimka’s solid-array
photostereograms such
as Emperor
Penguins
and Shamrock
are my favorites and inspired me to try to construct a
photostereogram of my own. I began
with a photograph I took at Mile
Rock Beach (San Francisco, California, USA), made a vertical
strip of it tileable, and manually constructed a depth map
rock-by-rock. I consider the result not too bad for a first
attempt. |
 |
Number One |
This simple mapped-texture stereogram is in fact the product of
some sophisticated software. I started with (poorly aligned)
left-eye and right-eye smartphone photographs of my own hand and
arm, inferred a depth map from these, and used the original images
to smoothly texture a stereogram generated from that depth map. |
 |
Upward Shapes |
Like Rotated Squares and Sinking
Ship, Upward Shapes fits in the How does this even
work? category. It’s an object-array stereogram in which the
objects are laid out at a slight upward angle (5°) instead of
horizontally. Strangely, the 3‑D effect still works. |
 |
Self Stereo |
An object-array stereogram typically comprises one or more
objects that repeat at varying intervals to produce the illusion of
depth. Self Stereo is an experiment in using
a single, solid-looking object that itself consists of a
repeated pattern. The single-object construction turned out to be
less impressive than I had hoped, but the 3‑D effect involving
the solid structure came out fine. |
 |
Bottle and Fishes 3‑D |
As an initial test of some new software I wrote for generating
mapped-texture stereograms, I tried producing a stereogram version of
Georges
Braque’s Bouteille
et Poissons. It doesn’t look as much like the original as I
had hoped, but the 3‑D image is reasonable easy to perceive. |
 |
Bowling Ball and Pin |
In 2016 a book publisher wrote to me, asking if I could author a
stereogram coloring book for them. I said no because (a) I had
no idea how to produce a color-your-own stereogram and (b) they
wanted 48 images, which would have taken me an eternity to produce.
With Bowling Ball and Pin (also available
in SVG and PDF),
I’ve at least addressed issue (a).
A sample coloring (also available
in SVG) shows what the result
might look like. |
 |
Lava Lamp |
What colors do you see in this image? Amazingly, the image uses
only pure red, pure green, pure blue, and light gray—plus a
black outline around each shape. Zoom in if you don’t believe me!
This effect, in which our perception of color is influenced by
surrounding colors, is known as
the Munker-White
illusion or
the Bezold
effect. An SVG version of Lava
Lamp is also available. |
 |
Balloons Above the City |
This stereogram enhances the basic mechanism employed
by Self Stereo with a more varied 3‑D view. I really
like how the buildings all appear to have the same height in the
2‑D image but different heights in the 3‑D image. (As
an aside, no one will ever hire me as a city planner because I’d
insist that buildings form a stereogram when viewed from
above. 😀) |
 |
Ghost in the Doorway |
I’ve long struggled to find a way to include transparent objects
without making the 3‑D hard to focus on. Ghost in the
Doorway is my best attempt so far. The intention is for the
ghost to be only partially visible but the doorway to look solid. I
think this came out reasonably well given the difficulty of the
task. |
 |
Eyeglasses |
Can a stereogram’s 2‑D image transition between crisp and
blurry without disrupting the 3‑D image? Eyeglasses
indicates that the answer is yes. Notice how the background is very
blurry, the frames of the eyeglasses are slightly blurry, and the
view through the lenses is perfectly crisp. Nifty, eh? |
 |
Willis Tower |
This stereogram, of
Chicago’s Willis
Tower (or Sears Tower, as it was called when I was growing up),
implements a similar concept to Empty Table, above: varying
brightness within an image. In Empty Table, the shadow
spreads evenly throughout the picture. Here, I wanted to see if I
could localize the shadow to the central 3‑D object. It was
also an interesting challenge to devise a 2‑D texture that
draws out the boxy structure of Willis Tower within a stereogram’s
low effective resolution. |
 |
Pair of Shoes |
I wanted to see if I could construct a stereogram entirely of
horizontal and vertical lines—no curves and no diagonals.
These lines further form a single path with no self-intersections
(à la String Theory, above).
An SVG version of Pair of
Shoes is also available. |
 |
Sea Star on the Sand |
What makes this stereogram unique is the 2‑D texture.
Inspired by the album art for
Soulwax’s Any
Minute Now, it portrays the word STAR when viewed at a
distance. (I find it’s easier to perceive when viewed at an angle
of about 45°.) |
 |
Stacked Blocks |
This stereogram shares a bit in common with Sinking
Ship and Eyeglasses above. In the case of Stacked
Blocks, the 2‑D texture is crisp in the horizontal center
of the image but becomes increasingly pixelated toward the left and
right edges. Because the basic coloring is preserved as single
pixels morph into 2×2 regions then 4×4, 8×8,
16×16, and finally 32×32, the image is relatively easy
to perceive apart from the leftmost and rightmost blocks. |
 |
As American as Apple Pie |
You may have noticed that String Theory and Pair of
Shoes use a line that zigs and zags alternately top-to-bottom
and bottom-to-top. I wondered if it would be possible instead to
meander alternately left-to-right and right-to-left. It is!
However, in the interest of producing a more aesthetically pleasing
stereogram, I ended up forgoing the single-line technique for As
American as Apple Pie. Instead, I drew a number of wavy
horizontal lines, colored the interstitial space, and tossed in some
stars to produce a reasonably accurate American flag.
An SVG version of As American as
Apple Pie is also available. |
 |
Trigonometry |
I had long thought about constructing a mathematical function
that can be viewed as a stereogram when plotted. My early attempts
were based on interpolation, but this led to excessively complex,
numerically unstable functions. The function plotted
in Trigonometry was constructed manually and is much, much
simpler: cos(10𝜋(1−|x|)5/4). The downside is
that the 3‑D image is also disappointingly simple.
An SVG version
of Trigonometry is also available. |
 |
Tetrominoes |
Here’s an object-array stereogram of the five
free
tetrominoes (think Tetris), rendered using transparent glass
versions of the eight
tetracubes.
What worked: intersecting transparent objects.
What didn’t work and was therefore removed from the
final image: larger objects (too hard to discern the 3‑D
image) and shadows (too distracting). Contrast Tetrominoes
with an earlier version and see
for yourself. |
 |
Crisscross |
I stumbled across the effect used in this animated (20-second
loop) object-array stereogram by accident. When viewed in
3‑D, the cyan stripes appear on top, the magenta stripes on
bottom, and the yellow circles between them. If the yellow circles
are removed, the cyan and magenta stripes appear to lie in the same
plane. Weird, huh? An SVG version
of Crisscross with nicer, smoother animation is also
available. |
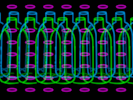 |
Shampoo and Conditioner |
This is my first attempt at creating a contour stereogram so I
intentionally kept it a bit simple. I slightly darkened the back
side of each bottle, which is a subtle but pleasant effect.
An SVG version of Shampoo and
Conditioner is also available. |
 |
Snow Globe |
Some of the best stereogram artists superimpose contours atop
conventional or mapped-texture stereograms to expose details in the
3‑D model and make the overall image easier to perceive.
(Contrast Snow Globe with
no contours and no mapped textures.) The idea in Snow
Globe, which I don’t believe I’ve seen previously, is
additionally to use contours to delineate transparent regions, in
this case the globe itself. I’m glad that the snowflakes are quite
visible—I was worried that they wouldn’t show up, and I’d have
a snowless snow globe. |
 |
Dalí Hypercubus |
I’ve been trying to improve upon the technique used above
in Big Snake Mouth and Pretzel Maze, in which a
stereogram is produced by warping a tiled image. The goal is to
avoid ugly discontinuities in the 2‑D image. Dalí
Hypercubus is not yet perfect—the edges in the 3‑D
image aren’t as crisp as they ought to be—but it is an
improvement. In particular, the new technique supports sudden
changes in depth, which prior techniques did not. The stereogram
name refers
to Salvador
Dalí’s Corpus
Hypercubus, and the 2‑D image comprises photographs
and self-portraits of Dalí. |
 |
The Land of Ribbons |
This stereogram depicts a stylized hill, cloud, and sun. each
defined by a single, colored ribbon. The interesting bit is how the
white ribbon comes to the front to form the cloud then recedes so
the yellow ribbon can come to the front to form the sun. |
 |
Duck Shoot |
A number of Gene Levine’s
stereograms embed a stereogram within non-stereogram
surroundings, which makes it non-obvious that the image is in fact a
stereogram. I wanted to try that trick myself. As a bonus, I
rendered the 3‑D image using a combination of a
SIRDS, a
contour stereogram, and a cloud (small-object) stereogram. |
 |
Watering Can |
The 2‑D image seen here, derived
from Renoir’s A
Girl with a Watering Can, is
what Øyvind Kolås
has dubbed
a color
assimilation grid illusion . That is, while the image
appears to be a bit faded but colored more-or-less normally
(especially when viewed at a distance), it is in fact 88%
gray—your brain is filling in the missing colors. It’s nice
that the effect works fine even though the colored-hatch pattern is
a bit distorted due to the stereogram. |
 |
Funhouse Mirrors |
I’m still trying to improve my techniques for minimizing
horizontal discontinuities in a stereogram’s 2‑D image. Here
you see my latest attempt. Although I’m pleased with the 2‑D
view, I still haven’t managed simultaneously to include sufficiently
sharp edges in the 3‑D image. To clarify, I refer you
to a conventional rendering
of Funhouse Mirrors in which the 3‑D view is nice
and crisp, but the 2‑D view chops segments out of the people
(most noticeably with the male models). |
 |
Japanese Teapot |
I know you’re tiring of hearing me say this, but
I’m still trying to improve my techniques for minimizing
horizontal discontinuities in a stereogram’s 2‑D image. I’ve
been making good progress, as you can see by the lack of
distracting, sharp, vertical lines in the 2‑D image shown here
(a tiled derivative
of Hiroshige’s View
of the Whirlpools at Awa). Pixels are stretched and squashed,
rather than kept or discarded, to form the 3‑D image. I’ve
also produced
a new Dalí
Hypercubus and
a new Funhouse
Mirrors. Contrast the smoothness of the old and new
2‑D images and the sharpness of the edges in the old and new
3‑D images. |
 |
Palette and Brush |
What’s the narrowest 2‑D tile that still leads to a
perceptible 3‑D image? More formally, what are the minimum
pixel widths of an autostereogram’s near and far planes? I was able
to go as low as 21 pixels on the near plane and 32 on the far plane,
as used in the image presented here. (I included guides at the top
to help my eyes diverge the desired amount, but it’s still not easy.
How do your eyes fare?) I also created a
WebP animation of Palette and
Brush, which repeatedly varies the near/far separation from
85/128 down to 21/32 and back. Note that only the 2‑D is
stretching and squashing. Changes in the width of the 3‑D
image are an optical illusion. |
 |
Cat and Mouse |
Does rendering a stereogram with a
halftoning
pattern make the 3‑D image hard to perceive? Answer: no. In
fact, this is actually one of my clearer works.
An SVG version of Cat and
Mouse, comprising 31,510 little, black circles, is also
available. |
 |
Theater Masks |
Is it possible to encode different stereograms into an image’s
different color channels? I considered specifically
the HCL
color space, encoding different stereograms in the hue, chroma,
and lightness channels. What I discovered is that only the
lightness stereogram, a comedy mask, is visible. But be sure
to watch the Theater Masks
video, in which I gradually set lightness to a uniform value,
which makes the hue stereogram, a tragedy mask, visible. Then I
gradually set hue to a uniform value, making the chroma stereogram,
a star, visible. |
 |
Two Jack-o’-Lanterns |
The shadow on the green ribbon in The Land of Ribbons
above got me thinking: Could one construct an object-array
stereogram in which the objects’ shadows form the 3‑D
image? In Two Jack-o’-Lanterns, the left jack-o’-lantern
is composed from shadows lying behind a flat wall of objects. The
right jack-o’-lantern is the opposite, composed from objects lying
in front of a flat wall of shadows.
An SVG version of Two
Jack-o’-Lanterns is also available. |
 |
Transparent Egg |
Lovesick, above, combines front and back
stereograms for a richer 3‑D effect. I began wondering if
more than two stereograms could be combined in that
manner. Transparent Egg depicts an egg with separate
stereograms for the front and back of the shell and the front and
back of the yolk. I’ll claim a partial success on this one. All
four components are indeed visible, but they’re a bit hard to
perceive in places. An SVG version
of Transparent Egg is also available. |
 |
Camping Tent |
Can one create a stereogram that is also
a connect-the-dots
puzzle? The answer is yes, but with qualifications.
Try as I might, I was unable to achieve my goal of producing a dot
pattern that would not reveal the hidden image until the dots were
connected. Consequently,
the solution adds little to
the unsolved variant. An SVG version
of Camping Tent
and its solution are also
available. |
 |
Camouflage |
A hidden-image stereogram employs slight variations in a
repeated pattern to hide a 3‑D object. An object-array
stereogram, in contrast, repeats a visible object at different
distances to make the object instances appear at different
depths. Camouflage is unique in that it is an object-array
stereogram in which the repeated object (a military rifle)
is not visible—because it’s camouflaged against the
background. I’m pleased with how this stereogram turned out. |
 |
Hats |
Stained-glass stereograms are among the easiest types of
autostereograms to perceive and a great choice for beginners. My
plan is to improve automation of the process of producing this type
of stereogram. Hats is a largely manual effort I undertook
to get a feel for the touch-ups I eventually want the computer to
perform. |
 |
Fish Tank |
The idea here was to see what would happen if I overlaid a
transparent object-array stereogram atop a random-dot stereogram
such that the visible objects in the former cut through the hidden
object in the latter. Would the hidden object appear partially
transparent? The answer is sort of. I find the effect
more distracting than pleasing, and I also find it hard to gauge the
relative depths of some of the individual objects. Oh, well; it was
worth a try. |
 |
Space Invaders |
An object-array stereogram normally constructs a 3‑D
effect by repeating an object at different horizontal
intervals. Space Invaders is unique in that the objects
are (mostly) evenly
spaced—see the underlying
grid—but are altered slightly so that some objects appear
to pop out while the rest appear flat. As the alien ships form only
an 11×6 grid of pixels there’s not enough resolution to
draw more than simple geometric shapes so don’t expect anything too
fancy here. |
 |
Swarm of Bees |
I finally figured out why the 3‑D for the toys
in Child’s Play, above, appears a bit off: When 3‑D
floaters are used in an object-array stereogram, they have to be
rotated in the opposite direction from an ordinary
perspective rendering. Swarm of Bees correctly rotates the
bees so that each bee displays proper depth when viewed
wall-eyed. |
 |
X Marks the Spot |
The objects in an object-array stereogram normally span the
width of the image. This made me wonder if it would be possible for
the objects not to span the width of the image but rather
to fade out after a few repetitions. I find the effect works better
for the contiguous objects near the center of the X than for
the sets of objects near the top and bottom of the X that
fade out and fade in again. |
 |
Bunch of Bananas |
This is an experiment to see if I could construct a random-dot
stereogram in which only one color pops up and the rest form the
background. (From the stereogram title you can probably guess which
color is special. 😀) Being made of speckles, the 3‑D object
is not fully solid, but I find that it is reasonably
recognizable. |
 |
Acorn |
A visitor to this site asked about very, very small stereograms.
Acorn is my attempt to produce a 100×100-pixel
random-dot stereogram—a bit larger than a typical postage
stamp. The 3‑D is a bit hard to focus on, and it may not
obviously appear to be an acorn, but I hope you can see that
there’s something present in the image. If you give up,
a full-size version of Acorn
(1000×1000 pixels) is also available. |
 |
Driving Accident |
This stereogram is essentially a more sophisticated version of
Sombrero, above. The technical approach was to construct
an object-array stereogram of a warped plane from individual points
rather than complete objects then to connect those points in a
lattice to produce a seamless fence. This solid-array stereogram is
overlaid atop both a contour stereogram and a patterned stereogram
of a car. |
 |
Desperation |
Desperation is similar in spirit to Two Monets
above but with an attempt to make the 3‑D image (a noose
hanging from the ceiling) a bit more perceptible by drawing it as a
SIRDS with a
visible diagonal-line bias and by reducing the contrast of the
overlaid 2‑D image (Courbet’s
Le
Désespéré). This helps, but there
remains a lot of room for improvement. |
 |
Secret Message 3 |
Here’s another flickery stereogram; sorry. Like Secret
Message and Secret Message 2 above, the challenge
is to see if you can read the hidden word. The experiment I’m
performing is to see if an object-array stereogram can split its
objects into thirds and let the viewer’s eye recombine them.
An SVG version of Secret
Message 3 is also available. |
 |
Petri Dish |
This is an object-array stereogram that uses one set of shapes
for the foreground and one for the background, but—and this is
what makes Petri Dish unique—merges foreground and
background shapes when they overlap. Thus, individual shapes can
contribute to both the foreground and the background layers.
Furthermore, object merging leads to less exact repetition than in a
conventional object-array stereogram.
An SVG version of Petri Dish
is also available. |
 |
Barn and Silo |
This image furthers the technique developed for Land of
Ribbons above by employing multiple shades of color to more
clearly disambiguate side-by-side objects, in this case a red barn
and a gray silo. I would have liked to have been able to make the
objects denser (using more vertical lines) to make them more easily
perceptible, but that would have made it harder to distinguish the
two objects. An SVG version of Barn and
Silo is also available. |
 |
Noah’s Ark |
This is a rather mundane stereogram of an ark. What’s
noteworthy is the software used to produce it: I
used libmorph to warp
a regularly tiled pattern into the stereogram you see here. Why is
that interesting? Because the same mechanism can be used to
smoothly morph one 3‑D image into another as in
this Noah’s
Ark morphing stereogram video (q.v.). |
 |
Shower Stall |
This represents a new approach to including transparent objects
in a stereogram. I encoded the transparent objects using only the
hue and chroma color channels, not the lightness color channel.
This makes it possible to see through the glass face of the shower
stall into the opaque interior (which contains just a bench). I
like this approach and might reuse it in the future. |
 |
Lighthouse |
Here’s a stereogram of a lighthouse that encodes a secret
message. Unlike Secret Message, Secret
Message 2, and Secret Message 3 above, the
message is encoded in the 2‑D image, not the 3‑D image.
Hence, even people who can’t perceive stereograms can enjoy this
puzzle. Hint #1: Read down the center
column. Hint #2: Look in the negative
space. Hint #3: Try squinting/closing your eyes
partway. An SVG version
of Lighthouse is also available. |
 |
Scissors |
Most stained-glass stereograms delineate their 3‑D objects
with contour lines. Doing so facilitates perception of the
3‑D objects, especially small or thin objects. My goal in
creating the Scissors stereogram was to achieve a
comparable effect using only abrupt color changes—no contour
lines. I think the stereogram came out pretty crisp, don’t you? |
 |
Bell, Book, and Candle |
The idea here was to see if I could create a stereogram
that looks like an object-array stereogram, but only one
instance of each identifiable object pops out in 3‑D; the rest
blend into the smooth background object. I claim success in
achieving that effect. |
 |
Zebra |
Ilja Klemencov's “They can disappear” hides
the WWF's panda logo
within a zigzag pattern. Although I was able to mimic this effect
in a self portrait (try viewing it at
an angle), I wondered if I similarly could hide a stereogram. After
a number of attempts I concluded, “Yes, but not as
nicely”. Zebra is a stereogram comprising 176 evenly
spaced zigzags in which the pen thickness varies
substantially—I was aiming for subtly—as the line moves
down the page. An SVG version
of Zebra is also available. |
 |
House with Fence |
The fence in this stereogram's foreground is in fact a hidden
message (in 2‑D). View the image from the bottom at a very
shallow angle or, alternatively, save the image to a file and use
your favorite image editor to scale it down to 70 pixels tall while
retaining the existing width. |
 |
Mardi Gras Mask |
This is partly an attempt to construct a contour stereogram with
vector graphics and partly a test of drawing beads that don't
perfectly line up horizontally. The result is kind of so-so: the
mask's details (e.g., its outline and where the eye holes lie) are a
bit hard to perceive, but it's not too difficult to tell that
there's something there. An SVG
version of Mardi Gras Mask is also available. |
 |
Birthday Cake |
This is an experiment with color. The candle bodies and the
stripe of frosting are supposed to appear to use a darker shade of
orange than the candle flames and the cake but are in fact the same
shade of orange. (The only colors in the image
are ◼, ◼, and ◼.) I find the stereogram itself isn't all
that interesting, alas. |



















































































































